
Polinomio:
Los polinomios son fundamentales en el campo de las matemáticas y tienen aplicaciones en diversas áreas, desde la física hasta la economía. En este artículo, exploraremos en detalle qué son los polinomios, sus tipos, propiedades, operaciones y aplicaciones, así como su importancia en el análisis matemático.
¿Qué es un Polinomio?
Un polinomio es una expresión matemática que consiste en una suma de términos, donde cada término se compone de un coeficiente y una variable elevada a una potencia entera no negativa. Los polinomios se pueden expresar en la forma general:
P(x)=anxn+an−1xn-1+…+a1x+a0
Donde:
- P(x) es el polinomio.
- an,an−1,…,a0 son coeficientes (números reales o complejos).
- n es un número entero no negativo que representa el grado del polinomio.
Tipos de Polinomios
Los polinomios se pueden clasificar de varias maneras, dependiendo de su grado, número de términos y otros criterios.
Según el Grado
- Polinomios de grado 0: Constantes (ejemplo: P(x)=5.
- Polinomios de grado 1: Lineales (ejemplo: P(x)=2x+3).
- Polinomios de grado 2: Cuadráticos (ejemplo: P(x)=x2−4x+4).
- Polinomios de grado 3: Cúbicos (ejemplo: P(x)=x3+2x2−x+1).
- Polinomios de grado 4 y superiores: Cuárticos y más (ejemplo: P(x)=x4−3x3+2x2−x+1).
Según el Número de Términos
- Monomios: Un solo término (ejemplo: 3x2).
- Binomios: Dos términos (ejemplo: x2+4x).
- Trinomios: Tres términos (ejemplo: x2−3x+2).
- Polinomios: Más de tres términos.
Propiedades de los Polinomios
Los polinomios tienen varias propiedades que son importantes para su manipulación y análisis.
Cierre Bajo la Suma y Multiplicación
La suma y multiplicación de polinomios también produce un polinomio. Por ejemplo, si P(x)P(x) y Q(x)Q(x) son polinomios, tanto P(x)+Q(x)P(x)+Q(x) como P(x)⋅Q(x)P(x)⋅Q(x) serán polinomios.
Grado del Polinomio
El grado de un polinomio es el exponente más alto de la variable en su expresión. Por ejemplo, en el polinomio 3x4+2x3−x+5, el grado es 4.
Coeficiente Principal
El coeficiente principal es el coeficiente del término de mayor grado. En el ejemplo anterior, el coeficiente principal es 3.
Operaciones con Polinomios
Las operaciones básicas que se pueden realizar con polinomios incluyen la suma, resta, multiplicación y división.
Suma de Polinomios
Para sumar polinomios, simplemente se suman los coeficientes de los términos semejantes. Por ejemplo:

Resta de Polinomios
La resta de polinomios se realiza de manera similar a la suma, restando los coeficientes de los términos semejantes:

Multiplicación de Polinomios
La multiplicación de polinomios se hace usando la propiedad distributiva. Por ejemplo:
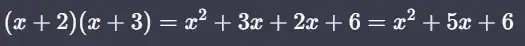
División de Polinomios
La división de polinomios puede ser más compleja y a menudo se realiza usando la división sintética o la larga. Por ejemplo, para dividir:
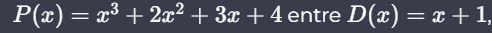
Se puede realizar una división larga.
Aplicaciones de los Polinomios
Los polinomios son utilizados en una variedad de campos, incluyendo:
Ciencias Naturales
En física, los polinomios se utilizan para modelar fenómenos naturales, como la trayectoria de un proyectil. La ecuación de movimiento puede ser representada por un polinomio.
Economía
En economía, los polinomios pueden describir comportamientos de oferta y demanda, así como la optimización de recursos.
Ingeniería
En ingeniería, los polinomios se aplican en análisis estructural, diseño de sistemas y control automático.
Informática
Los algoritmos de computación a menudo utilizan polinomios en sus cálculos, especialmente en el análisis de complejidad y procesamiento de datos.
Conclusión
Los polinomios son una parte esencial de las matemáticas y su comprensión es crucial para cualquier persona que desee estudiar matemáticas avanzadas o aplicar estos conceptos en campos científicos y técnicos. Desde su definición y clasificación hasta sus propiedades y aplicaciones, los polinomios son herramientas poderosas que nos ayudan a modelar y entender el mundo que nos rodea. Si deseas profundizar más en este tema, te animamos a explorar recursos adicionales y practicar la manipulación de polinomios a través de ejercicios.
