
Pirámide:
La geometría es una rama de las matemáticas que estudia las formas, tamaños y propiedades de las figuras en el espacio. Uno de los sólidos geométricos más fascinantes y estudiados es la pirámide. En este artículo, exploraremos en detalle qué es una pirámide, sus características, tipos, fórmulas y aplicaciones en el mundo real.
¿Qué es una Pirámide?
Una pirámide es un sólido tridimensional que tiene una base poligonal y una serie de triángulos que se unen en un punto común llamado vértice. La base puede ser de cualquier forma, como un triángulo, cuadrado, rectángulo o cualquier polígono. Las pirámides se clasifican principalmente según la forma de su base.
Características de las Pirámides
Las pirámides poseen varias características interesantes que las hacen únicas en la geometría:
- Base Poligonal: La base es el polígono que define el tipo de pirámide. Si la base es un cuadrado, se trata de una pirámide cuadrada. Si es un triángulo, es una pirámide triangular, y así sucesivamente.
- Vértice: Es el punto donde se encuentran todas las aristas laterales de la pirámide. Desde el vértice, se pueden trazar líneas que conectan con los vértices de la base.
- Aristas: Las aristas son los segmentos de línea que conectan los vértices de la base con el vértice superior, así como los lados del polígono en la base.
- Altura: La altura de la pirámide es la distancia perpendicular desde el vértice hasta el plano de la base.
Tipos de Pirámides
Las pirámides se pueden clasificar de diferentes maneras, pero una de las más comunes es según la forma de su base:
Pirámide Triangular
La pirámide triangular tiene una base que es un triángulo. Tiene tres aristas laterales y cuatro caras en total (tres triángulos y una base).
Pirámide Cuadrada
La pirámide cuadrada se caracteriza por tener una base en forma de cuadrado. Contiene cuatro aristas laterales y cinco caras (cuatro triángulos y una base cuadrada).
Pirámide Pentagonal
La pirámide pentagonal tiene una base con forma de pentágono y cuenta con cinco aristas laterales, sumando un total de seis caras.
Fórmulas Relacionadas con Pirámides
Entender las fórmulas que rigen las pirámides es fundamental para realizar cálculos relacionados con su volumen y área superficial.
Volumen de una Pirámide
La fórmula para calcular el volumen V de una pirámide es:
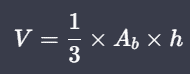
Donde Ab es el área de la base y h es la altura de la pirámide. Este cálculo es esencial en diversas aplicaciones, como la construcción y la planificación de espacios.
Área Superficial de una Pirámide
La fórmula para el área superficial A de una pirámide es:
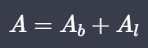
Donde Ab es el área de la base y Al es el área lateral. El área lateral se puede calcular sumando el área de todas las caras laterales.
Aplicaciones de las Pirámides en el Mundo Real
Las pirámides no solo son un concepto teórico en matemáticas, sino que tienen múltiples aplicaciones en el mundo real:
- Arquitectura: Las pirámides se han utilizado en la construcción de monumentos históricos, como las famosas pirámides de Egipto. Su diseño permite una distribución eficiente del peso y añade estabilidad.
- Diseño Gráfico: En el diseño gráfico, las pirámides pueden ser utilizadas como elementos visuales para representar jerarquías o estructuras de información.
- Geometría en la Naturaleza: Muchos cristales y estructuras naturales presentan formas piramidales, lo que demuestra la presencia de esta forma en el entorno natural.
Conclusión
Las pirámides son figuras geométricas fascinantes que han capturado la imaginación de matemáticos, arquitectos y artistas a lo largo de la historia. Comprender sus características, tipos y aplicaciones permite apreciar su importancia en diversas disciplinas. Desde la construcción de monumentos emblemáticos hasta su uso en cálculos matemáticos, las pirámides son un ejemplo perfecto de cómo la geometría se manifiesta en el mundo que nos rodea. Al estudiar las pirámides, no solo aprendemos sobre formas y volúmenes, sino que también exploramos la conexión entre las matemáticas y el mundo físico.
