
Ecuaciones:
Las ecuaciones son una de las bases fundamentales de las matemáticas y tienen aplicaciones en diversas áreas, desde la física hasta la economía. En este artículo, exploraremos en profundidad qué son las ecuaciones, los diferentes tipos que existen, cómo resolverlas y su relevancia en el mundo actual.
¿Qué es una Ecuación?
Una ecuación es una afirmación matemática que establece que dos expresiones son iguales. Se representa comúnmente en la forma ax+b=c, donde x es la variable que se desea resolver, y a, b y c son constantes. Las ecuaciones son esenciales en la resolución de problemas matemáticos y científicos, ya que permiten modelar situaciones reales.
Tipos de Ecuaciones
Existen varios tipos de ecuaciones, cada una con sus características y métodos de resolución:
Ecuaciones Lineales
Las ecuaciones lineales son aquellas que pueden representarse en la forma ax+b=0. Son de primer grado y su gráfica en un plano cartesiano es una línea recta. Ejemplo: 2x+3=7. Para resolverlas, se busca el valor de xx que satisface la igualdad.
Ecuaciones Cuadráticas
Las ecuaciones cuadráticas son de segundo grado y tienen la forma ax2+bx+c=0. Su resolución puede realizarse mediante factorización, la fórmula cuadrática o completando el cuadrado. Un ejemplo es x2−5x+6=0, que se puede factorizar como (x−2)(x−3)=0.
Ecuaciones Cúbicas
Las ecuaciones cúbicas son de tercer grado y se presentan en la forma:
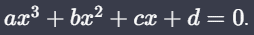
Pueden ser más complejas de resolver debido a la posibilidad de tener múltiples raíces. Por ejemplo:

Ecuaciones Diferenciales
Las ecuaciones diferenciales son aquellas que involucran funciones y sus derivadas. Se utilizan para modelar fenómenos en ingeniería, física y otras ciencias. Un ejemplo común es la ecuación de la población, que puede representarse como

donde P es la población y r es la tasa de crecimiento.
Métodos de Resolución de Ecuaciones
Resolver ecuaciones implica encontrar el valor de las variables que satisfacen la igualdad. Existen varios métodos para resolver diferentes tipos de ecuaciones:
Método de Sustitución
Este método es útil en sistemas de ecuaciones. Consiste en despejar una variable en una ecuación y sustituirla en otra. Por ejemplo, si tenemos y=2x+3 y x+y=10, sustituimos y en la segunda ecuación para obtener una sola variable.
Método Gráfico
El método gráfico implica representar las ecuaciones en un plano cartesiano. La solución se encuentra en el punto donde las gráficas de las ecuaciones se interceptan. Este método es particularmente útil para ecuaciones lineales.
Método de Igualación
Se utiliza para resolver ecuaciones cuadráticas. Consiste en igualar dos expresiones y resolver para la variable. Por ejemplo, al resolver x2=9, se puede igualar y luego calcular las raíces.
Aplicaciones de las Ecuaciones
Las ecuaciones tienen un papel crucial en diversas disciplinas. Aquí se presentan algunas de sus aplicaciones más relevantes:
En Ciencias Naturales
En física, las ecuaciones son fundamentales para describir leyes naturales, como la ley de gravitación de Newton, que se expresa mediante la ecuación:

Las ecuaciones también son esenciales en química para balancear reacciones.
En Economía
Las ecuaciones se utilizan para modelar comportamientos económicos, como la oferta y la demanda. Por ejemplo, la ecuación de la recta de oferta puede ser expresada como Qd=a−bP, donde Qd es la cantidad demandada y P es el precio.
En Ingeniería
Los ingenieros utilizan ecuaciones para resolver problemas prácticos, como el diseño de estructuras, donde deben considerar factores como la tensión y la compresión. Las ecuaciones diferenciales son particularmente útiles en este campo.
Conclusión
Las ecuaciones son un pilar fundamental en el ámbito de las matemáticas y sus aplicaciones en el mundo real son vastas y variadas. Desde resolver problemas simples hasta modelar fenómenos complejos, entender las ecuaciones es crucial para cualquier persona interesada en las ciencias, la ingeniería o la economía. Ya sea que estés estudiando para un examen o simplemente tengas curiosidad, dominar las ecuaciones te abrirá muchas puertas en tu camino académico y profesional.
